Biasanya anak-anak akan mengalami kesulitan saat diajak memecahkan soal perhitungan dimensi tiga. Harus kita kenalkan terlebih dahulu, apa itu jarak titik terhadap titik. Jarak titik terhadap garis. Jarak titik terhadap bidang, Jarak garis ke garis. dst.
Mari kita mulai dengan jarak titik ke garis.
Misalnya, tentukan jarak titik A ke garis PQ pada gambar berikut ini:
Sebelum kita membahas jarak A ke PQ, kita ajak murid memperhatikan percobaan yang saya lakukan di bawah ini.
Bu Rini: "Lihat, Bu Rini akan menjatuhkan spidol ini ke lantai! Jatuhnya kemana?"
Murid: "Ke bawah."
Bu Rini: "Mengapa tidak jatuh ke samping?" Lanjut saya sambil menjatuhkan spidol lagi.
Murid: "Karena pengaruh gravitasi bumi, Bu..."
Bu Rini: "Anggap garis PQ adalah permukaan tanah. Setiap benda yang jatuh, pasti akan jatuh ke bawah dengan arah tegak lurus dengan permukaan tanah."
Saya beri contoh sekali lagi dengan bola, dan langsung saya gambarkan di papan tulis.
Saya beri contoh sekali lagi dengan bola, dan langsung saya gambarkan di papan tulis.
Anak-anak akan mulai memahami jika sebuah benda jatuh, jatuhnya akan kemana.
Maka kita bisa mulai menerangkan jarak titik A terhadap PQ. Anggap A = bola, dan PQ = permukaan tanah. Maka titik A akan jatuh ke arah yang tegak lurus dengan permukaan tanah.
Maka jarak A terhadap PQ adalah jarak terpendek A terhadap garis PQ, yaitu AA'. Kita terangkan juga mengapa jarak terpendek merupakan garis tegak lurus? Kita ilustrasikan gambar di bawah ini, maka murid akan memahaminya.
Mereka akan tahu bahwa jarak terpendek adalah AA'.
Kita terangkan juga bahwa A' itu adalah proyeksi A terhadap garis PQ. Apa arti proyeksi? Jika titik A jatuh ke tanah (anggap tanahnya adalah PQ) jatuhnya pasti akan ke A'. Itulah makna proyeksi.
Murid akan merasa senang karena mereka tahu istilah baru, yang mungkin belum diajarkan di sekolah. Atau bisa jadi sudah diajarkan tapi tidak tahu maknanya apa.
Nah, murid sudah siap kita ajarkan apa itu diagonal bidang dan diagonal ruang.
Ingatkan rumus Phytagoras dan luas segitiga di bawah ini.
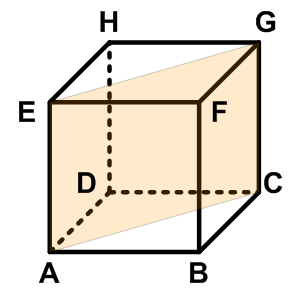
Kita jelaskan bagaimana penerapan rumus Phytagoras saat menghitung diagonal bidang dan diagonal ruang pada kubus di bawah ini.
Kita terangkan juga bahwa A' itu adalah proyeksi A terhadap garis PQ. Apa arti proyeksi? Jika titik A jatuh ke tanah (anggap tanahnya adalah PQ) jatuhnya pasti akan ke A'. Itulah makna proyeksi.
Murid akan merasa senang karena mereka tahu istilah baru, yang mungkin belum diajarkan di sekolah. Atau bisa jadi sudah diajarkan tapi tidak tahu maknanya apa.
Nah, murid sudah siap kita ajarkan apa itu diagonal bidang dan diagonal ruang.
Ingatkan rumus Phytagoras dan luas segitiga di bawah ini.
Kita jelaskan bagaimana penerapan rumus Phytagoras saat menghitung diagonal bidang dan diagonal ruang pada kubus di bawah ini.
Kita terangkan dengan konsep kesebangunan, akan didapatkan bahwa panjang EK = KL = LC
Contoh soal:
Berapakah jarak titik C terhadap bidang
BDG, jika rusuk kubus ABCD.EFGH = 8 cm?
Jawab:
Buat segitiga BDG dan bidang diagonal ACGE
Jarak C ke BDG adalah CL (jarak terpendek
dan syaratnya harus tegak lurus)
Sudah diperlihatkan pada rumus di atas
bahwa:
dan
Menghitung jarak titik ke titik dengan menggunakan vektor
Menghitung
jarak dari titik ke titik
Misalnya jarak A ke P
Dengan memakai prinsip vector, ambil jalan
saling tegak lurus menuju P, yaitu yang ditandai garis merah berikut ini:
Misal panjang sisi kubus = 8 cm
Maka jarak AP ditunjukkan oleh warna ungu,
sebagai jalan terpendek (pintas) mewakili rute merah.
Panjang garis AP bisa dihitung dengan rumus:
Sekarang
bandingkan dengan perhitungan manual memakai rumus Phytagoras
Langkah-langkahnya adalah:
1. Panjang AD = 8 cm, panjang DQ = 4 cm
2. Panjang PQ = 8 cm
Bandingkan dengan cara vector di atas,
hasilnya sama.
Pemakaian luas segitiga pada dimensi tiga
Dan untuk segitiga yang sama berlaku:
Rumus "alas x tinggi = ALAS x TINGGI" sangat berguna untuk menyelesaikan banyak
tipe soal dimensi tiga.
Contohnya
soal berikut ini:
Berapakah
jarak D ke TB?
Bagaimana penyelesaiannya? Lihat tahap demi tahap seperti yang ada pada slide di bawah ini.





















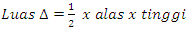




4 comments:
Thank you sir.
now i'm already know about "Dimensi tiga". Especially for "jarak".
terima kasih info cara mengajar yg sangat membantu.
Nc
Nc
Post a Comment